B Modélisation des signaux à la sonde autonome

B.1 Méthode

B.1.1 Les variables explicatives

Un premier travail a consisté à recueillir ou calculer des variables explicatives. Comme leur nom l’indique, ces variables sont supposées expliquer une partie de la variation des données.

Les variables explicatives utilisées dans ce chapitre sont présentées dans le tableau ci-dessous.

Variables explicatives	Acquisition
Hauteur d’eau	Modélisation des données bruts du SHOM
Coefficient de marée	SHOM
Vive eau / morte eau	Dérivé des données du SHOM
Dynamique de la marée (jusant/flot)	Dérivé des données du SHOM
Saisons	Manuellement
Ouverture ou fermeture des clapets	Détermination visuelle à partir des signaux

Au regard de la description du fonctionnement d’un système lagunaire (cf. section 2.4.1) les variables explicatives recueillies sont très limitées. Il manque notamment l’ensemble du volet de l’hydrologie continentale (débit des cours d’eau et de la nappe) ainsi que celui de de la climatologie (précipitation, température, évaporation et vent). La part de variations non expliquée sera donc potentiellement conséquente.

Les valeurs étant enregistrées par la sonde autonome toutes les 30 minutes, il est nécessaire que les variables explicatives possèdent la même fréquence. Il est possible d’élargir le pas de temps des signaux mais cela impliquerait une perte conséquente d’informations (pour rappel la durée moyenne d’un flot et d’un jusant est d’environ sept heures). Cela complique l’acquisition des données ; il est par exemple ardu d’acquérir un jeu de données de débit fiable à haute fréquence, d’autant que le bassin versant de l’Alanan n’est pas jaugé.

Les trois signaux (température de l’eau, conductivité et hauteur d’eau) ont été modélisés de la même façon. Nous illustrerons la méthode avec le signal de la hauteur d’eau.

B.1.2 Moyenne mobile

On commence par calculer une moyenne mobile afin d’enlever les imperfections liées à des phénomènes aléatoires enregistrés par la sonde. Une moyenne mobile simple se définit comme suit :

\[ \bar{x}_n = \frac{1}{N} \sum^{N-1}_{k=0}x_{n-k} \]

La figure B.1 présente une comparaison du signal obtenu avec le signal brut (il est recommandé de zoomer sur la figure pour observer l’effet de la moyenne mobile).

Figure B.1: Signal brut et moyenne mobile de la hauteur d’eau

B.1.3 Detrend

Dans l’objectif de rendre le signal stationnaire — prérequis à la modélisation de série temporelle — on detrend la série. Cette opération consiste à enlever sa tendance au signal. Nous avons également supprimé la saisonnalité à l’échelle de l’heure pour rendre le signal plus “lisible”. La tendance et les saisons sont détectées par une modélisation STL (cf. sections 4.1.3.1.1, 4.1.3.2.2, 4.2.1).

La figure B.2 présente le signal obtenu ainsi que sont autocorrélation temporelle³⁹. Cette dernière est importante et semble présenter une tendance polynomiale⁴⁰.

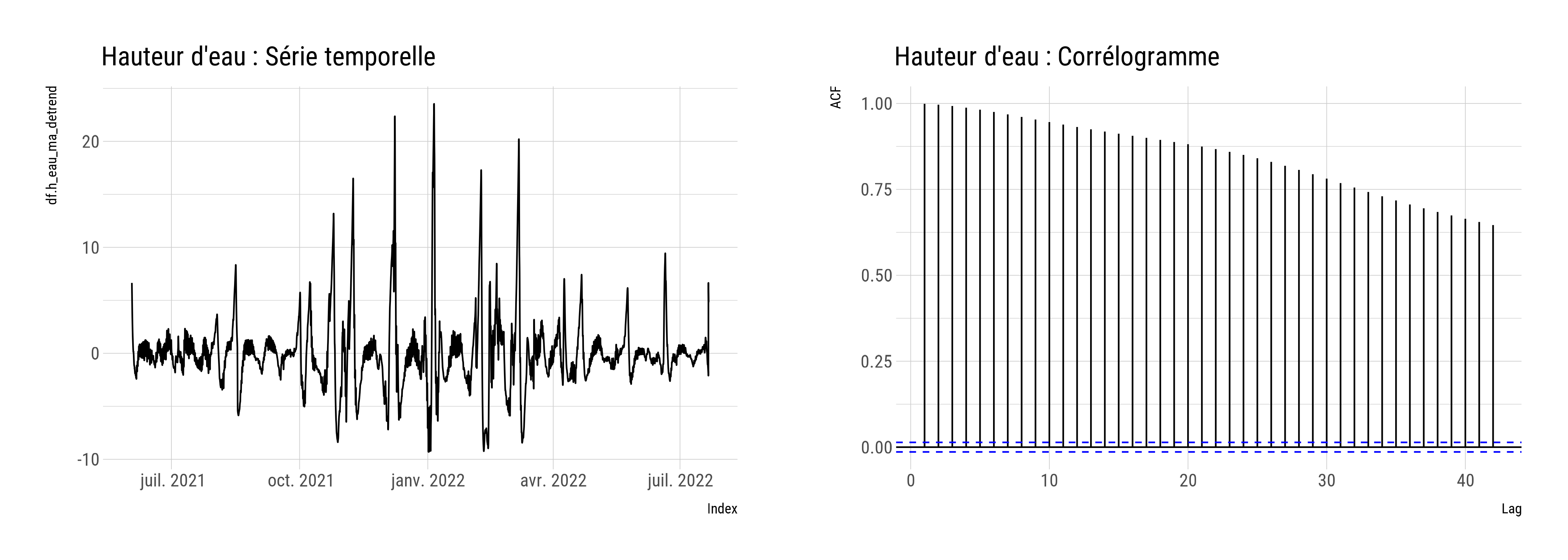
Figure B.2: Série temporelle et autocorrélation du signal de hauteur d’eau après detrend

B.1.4 Différenciation du signal

Pour supprimer la tendance polynomiale d’un signal temporel on peut effectuer une différenciation. Avec \(\Delta\) l’opérateur de différenciation \(\Delta y_t = y_t - y_{t-1}\). L’opérateur de différenciation d’ordre k correspondant est : \(\Delta^k y_t = \Delta(\Delta^{k-1} y_t)\).

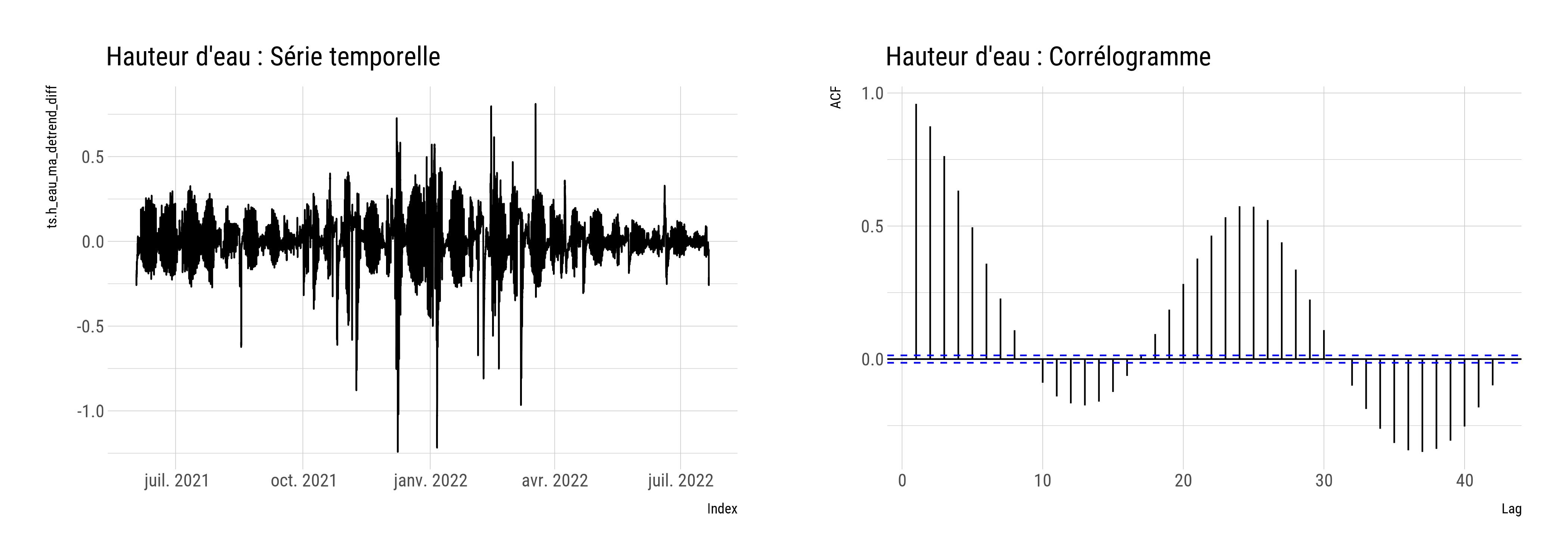
Figure B.3: Série temporelle et autocorrélation du signal de hauteur d’eau après différenciation

Le corrélogramme présente une variation particulière que l’on peut rapprocher du cycle de la marée (flot-jusant) (fig. B.3). Autrement dit, cela indique que les valeurs du signal à un instant \(t\) ont tendance à être corrélées avec elles-mêmes à un temps \(t-x\) suivant un schéma similaire à celui de la marée. Cette interprétation est également valable pour les signaux de température et de conductivité.

Enfin, nous effectuons de nouveau une moyenne mobile sur le signal. Cette dernière étape permet d’augmenter quelque peu l’efficacité du modèle.

B.1.5 Modèle Linéaire Généralisé (GLM)

L’effet des prédicateurs sur la variable a été évalué à l’aide d’un Modèle Linéaire Généralisé (l’abréviation GLM (Generalized Linear Model) est couramment utilisée).

Le GLM généralise la régression linéaire simple en permettant au modèle linéaire d’être relié à la variable réponse \(Y\) par une fonction lien \(g\) et en autorisant l’amplitude de la variance de chaque mesure d’être une fonction de sa valeur prévue, en fonction de la loi choisie.

\[ E(Y|X) = \mu = g^{-1}(X\beta) \]

où \(E(Y|X)\) est l’espérance mathématique de \(Y\) conditionnelle à \(X\). \(X\beta\) est le prédicateur linéaire (i.e. une combinaison linéaire de variables explicatives) et \(g\) une fonction lien. \(\mu\) est la moyenne de la distribution, dépendante de \(X\) (wikipedia, cons. 11/08/2022 13:36).

On a donc trois paramètres :

• Une distribution de la famille des exponentielles pour modéliser \(Y\)

• Un prédicteur linéaire \(\eta=X\beta\)

• Une fonction lien \(g\)

Sur R la fonction glm.fit a été utilisée. Les variables catégorielles ont été transformées en dummy variable (i.e. en variable numérique).

B.2 Résultats

B.2.1 Hauteur d’eau

Le modèle retenu est le suivant : h_eau.x ~ estimated + saison + maree_dyn + coef + clapets. La variable Vive-eau/Morte-eau a été supprimée.

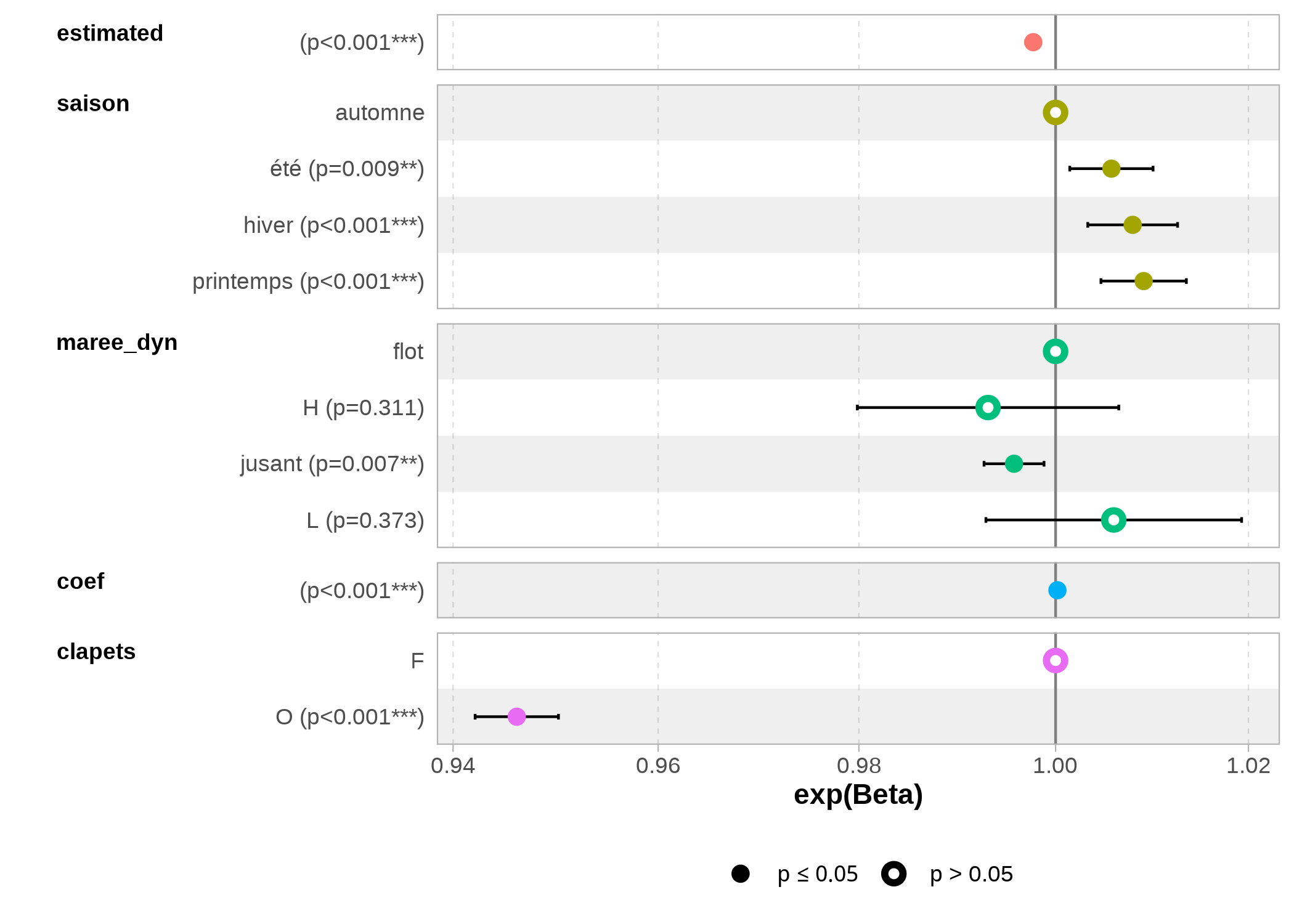
Figure B.4: Coefficient du modèle

On constate que l’ensemble des coefficients sont faibles excepté celui de la modalité ouvert de la variable clapets. Notons qu’il est normal que la \(p-value\) soit inférieur à \(\alpha = 0,05\) pour la première modalité de chaque dummy variable (fig. B.4).

Il peut paraître inattendu que la variable estimated (le signal de hauteur modélisé à Roscoff) explique peu la variabilité de la hauteur d’eau dans l’étang, dans la mesure où nous avons vu plus haut que le signal est autocorrélé avec un schéma correspondant à celui de la marée. Cela s’explique par le fait que le signal a été enregistré à un point relativement éloigné de Guissény et, surtout, que la marée doit-être “déformée” de manière significative à l’entré dans l’exutoire.
Une analyse visuelle de la superposition du signal de hauteur d’eau à Roscoff et à la sonde autonome permet d’émettre l’observation suivante : le signal de marée est “en retard” d’environ deux heures dans l’étang comparé à celui enregistré à Roscoff (fig. B.5). De plus, on constate que le signal à la sonde autonome est dissymétrique. Au flot, les hauteurs d’eau augmentent rapidement puis, au jusant, elles commencent à décroître de manière rapide avant de perdre progressivement en vitesse. Ainsi, dans une situation où les clapets sont ouverts, le flot à la sonde autonome dure environ 3 h et le jusant environ 9 h. Ce décalage est responsable, au moins en partie, de la faible corrélation entre les deux signaux calculés par les modèles présentés dans cette partie.
Dans ce cadre, il est logique que les variables maree_dyn et coef n’apportent que peu d’informations.

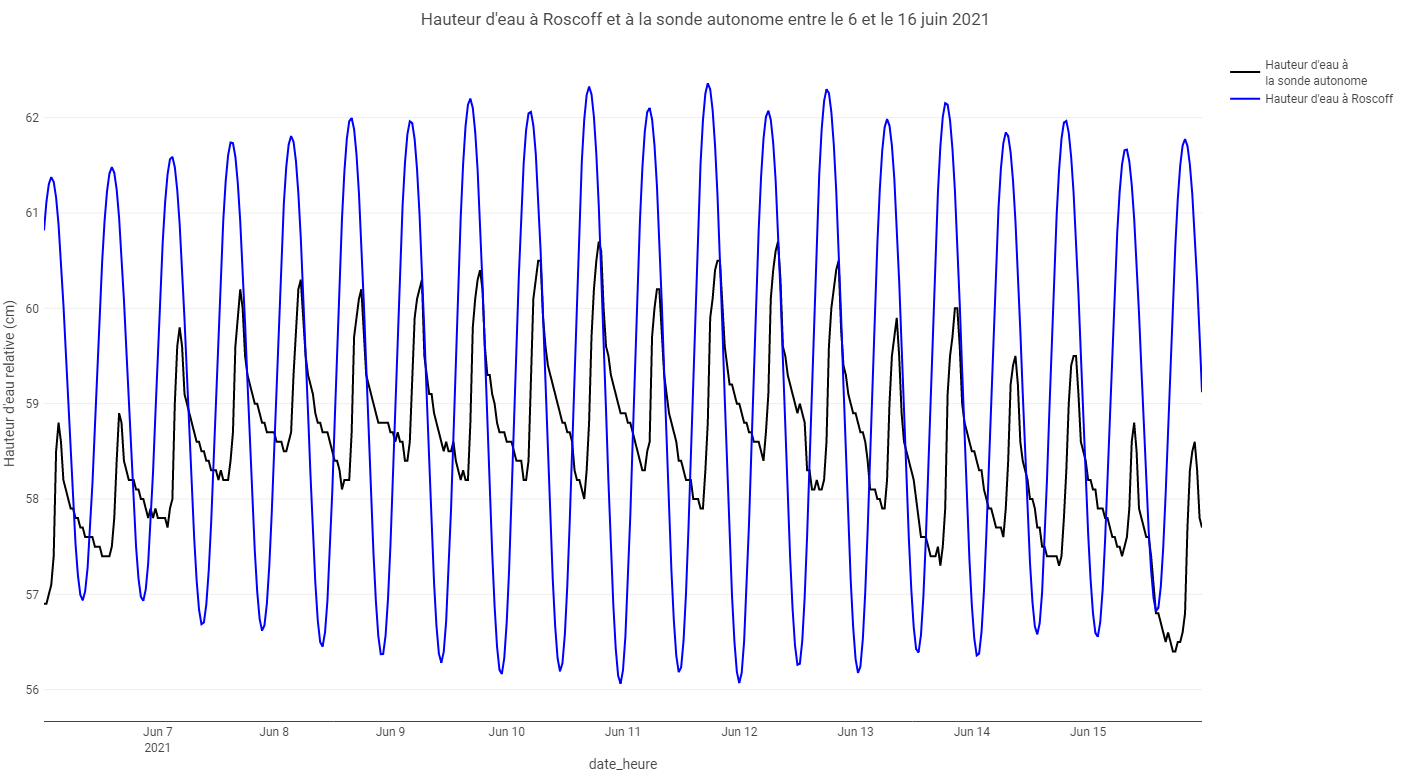
Figure B.5: Hauteur d’eau à Roscoff et à la sonde autonome entre le 6 et le 16 juin 2021

Finalement, au regard des résultats de la modélisation, seule la variable clapets possède un effet véritablement significatif et corroboré par l’observation sur la hauteur d’eau à la sonde autonome (fig. B.6).

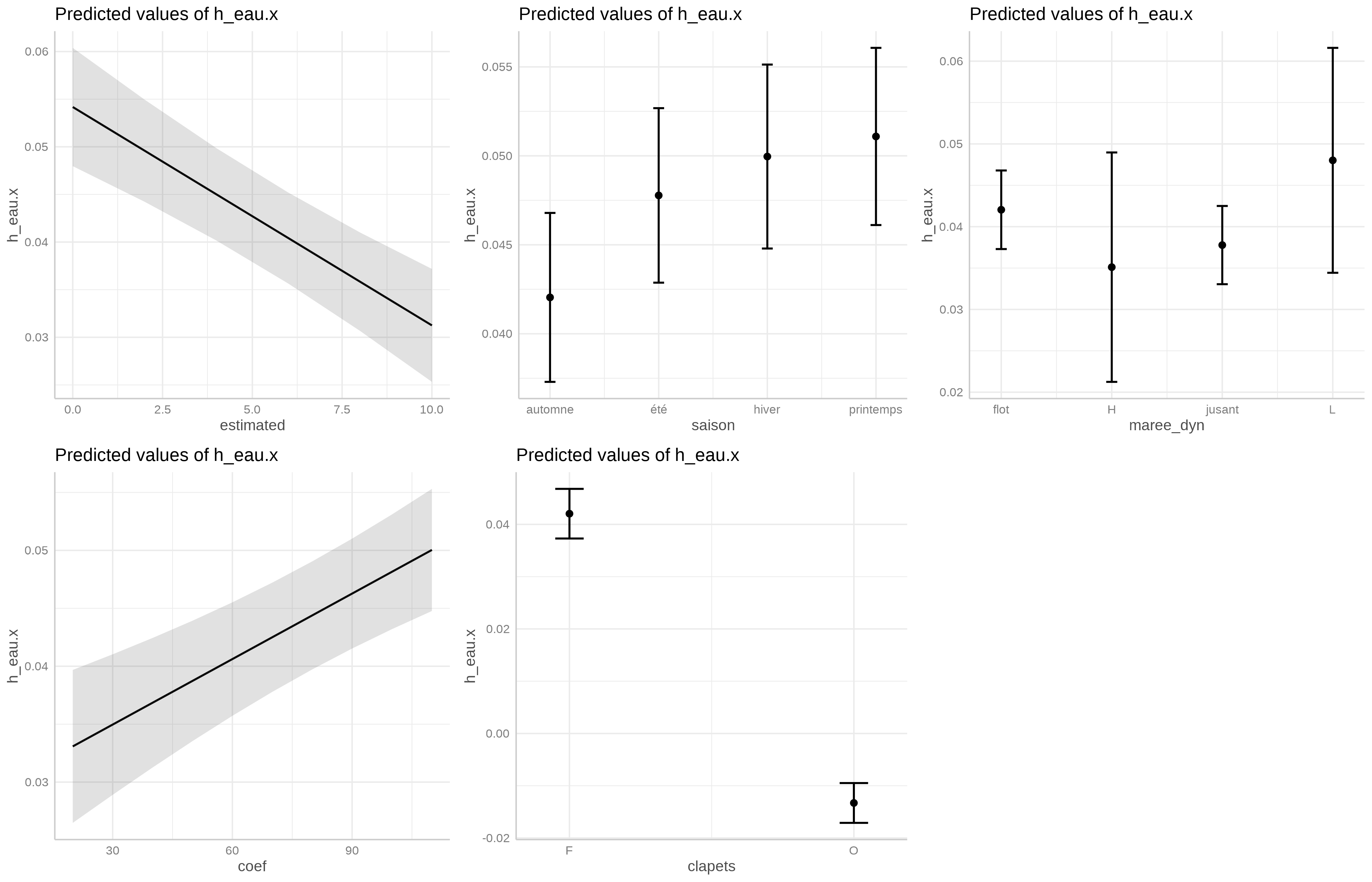
Figure B.6: Effet des prédicteurs sur la variable réponse

B.2.2 Conductivité

Le modèle retenu est le suivant : conduc.x ~ estimated + VE_ME + coef + clapets. La variable maree_dyn a été éludée dans ce modèle.

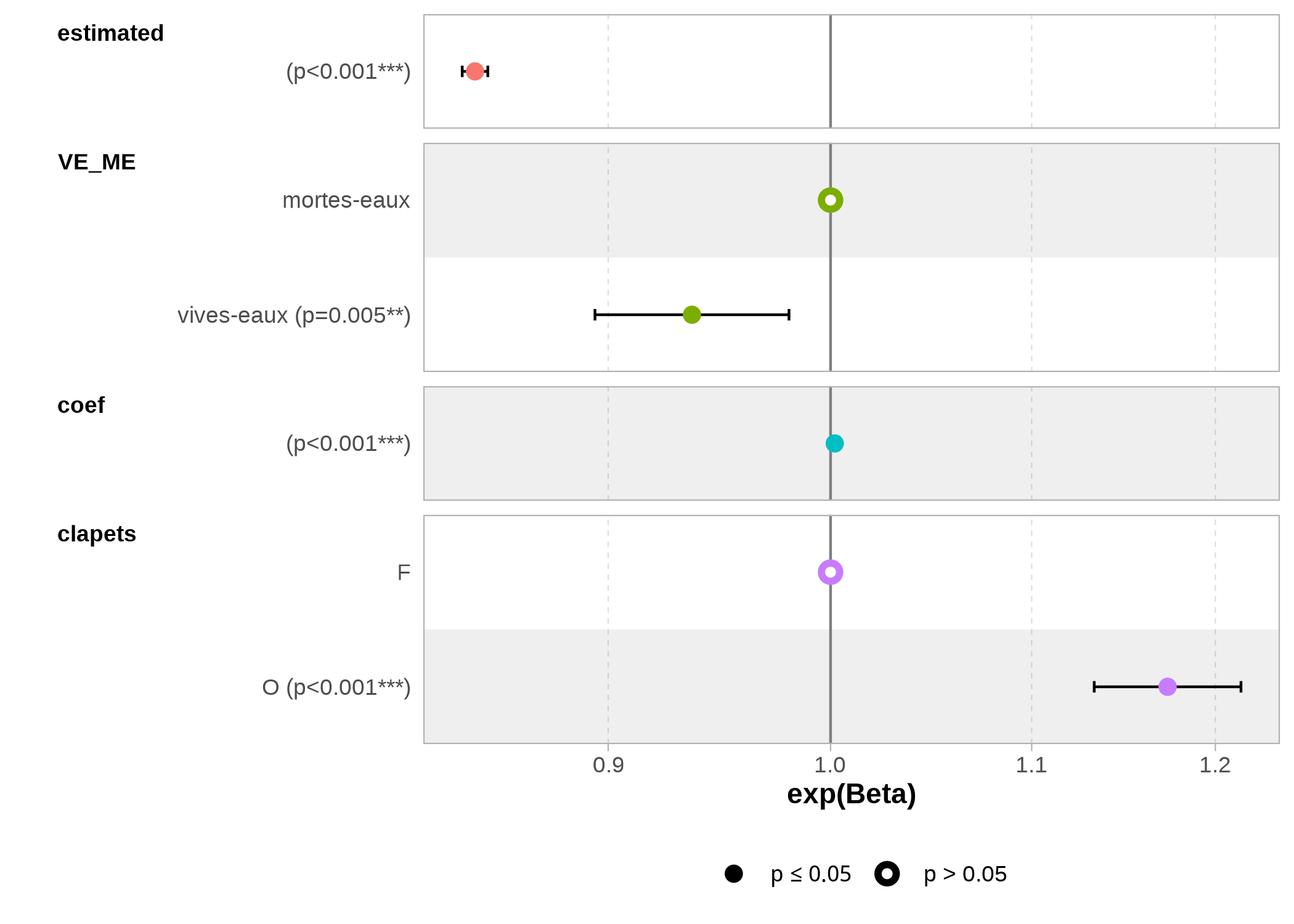
Figure B.7: Coefficient du modèle

La figure B.7 présente les coefficients du modèle. Comme nous l’avons plus haut, il ne semble pas évident d’interpréter la variable estimated étant donné la modification supposée du signal de marée à son entrée dans l’exutoire de l’étang. Dans ce cadre — les variables coefet VE_ME étant liées au phénomène de marée —, seule la variable clapets est raisonnablement interprétable. Ainsi, on observera des valeurs de conductivité plus élevées quand les clapets seront ouverts. En effet, comme indiqué dans la section 4.1.3.2.2, lorsque les clapets sont bloqués, l’apport d’eau douce induit une dilution des eaux marines engendrant une baisse progressive de la conductivité (fig. B.8).

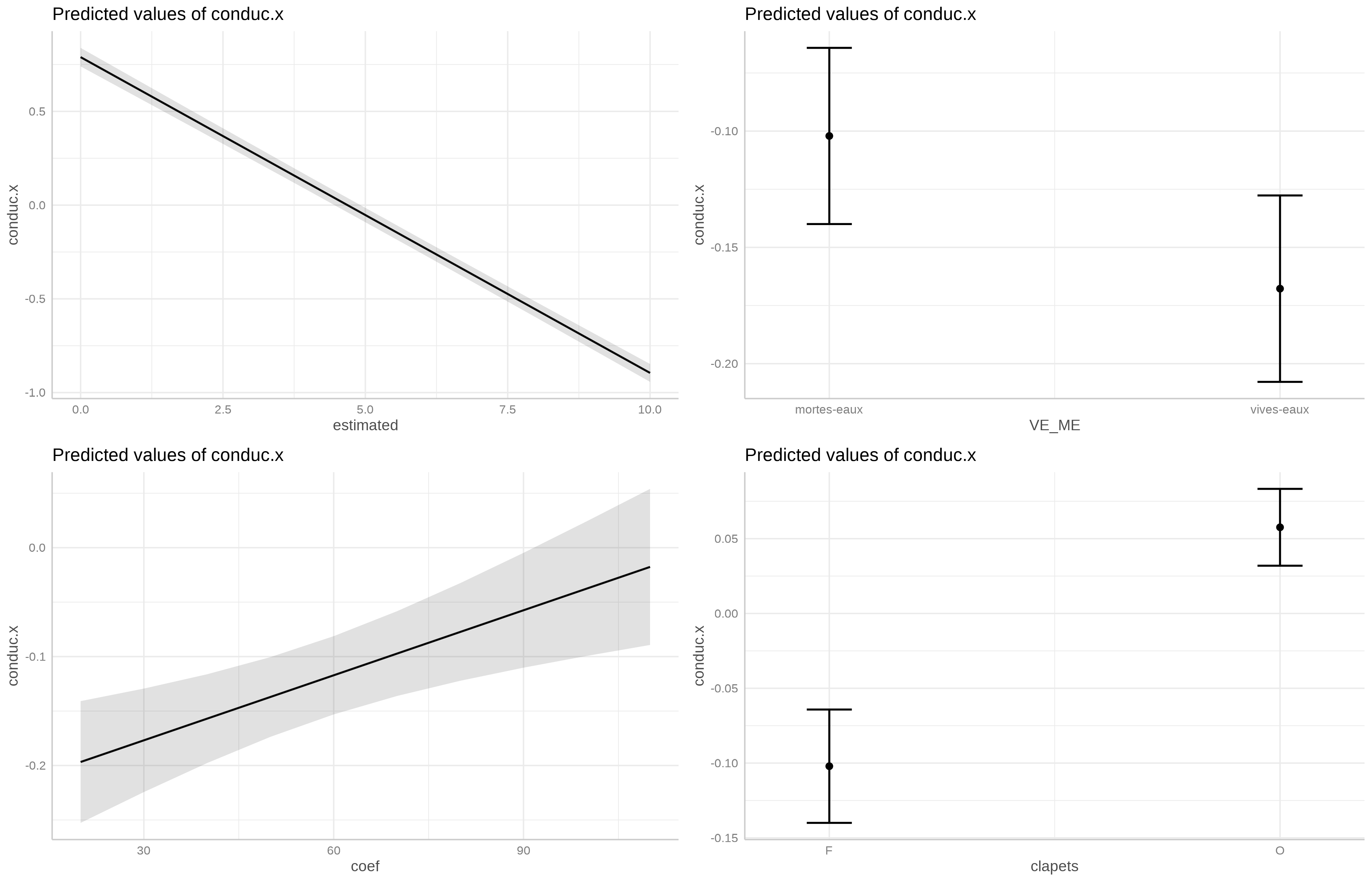
Figure B.8: Effet des prédicteurs sur la variable réponse

B.2.3 Température

La modélisation du signal de température ne semble pas donner de résultats probants, nous ne les présenterons donc pas ici. Comme indiqué plus haut, le signal est également autocorrélé sur le schéma de la marée (fig. B.9).

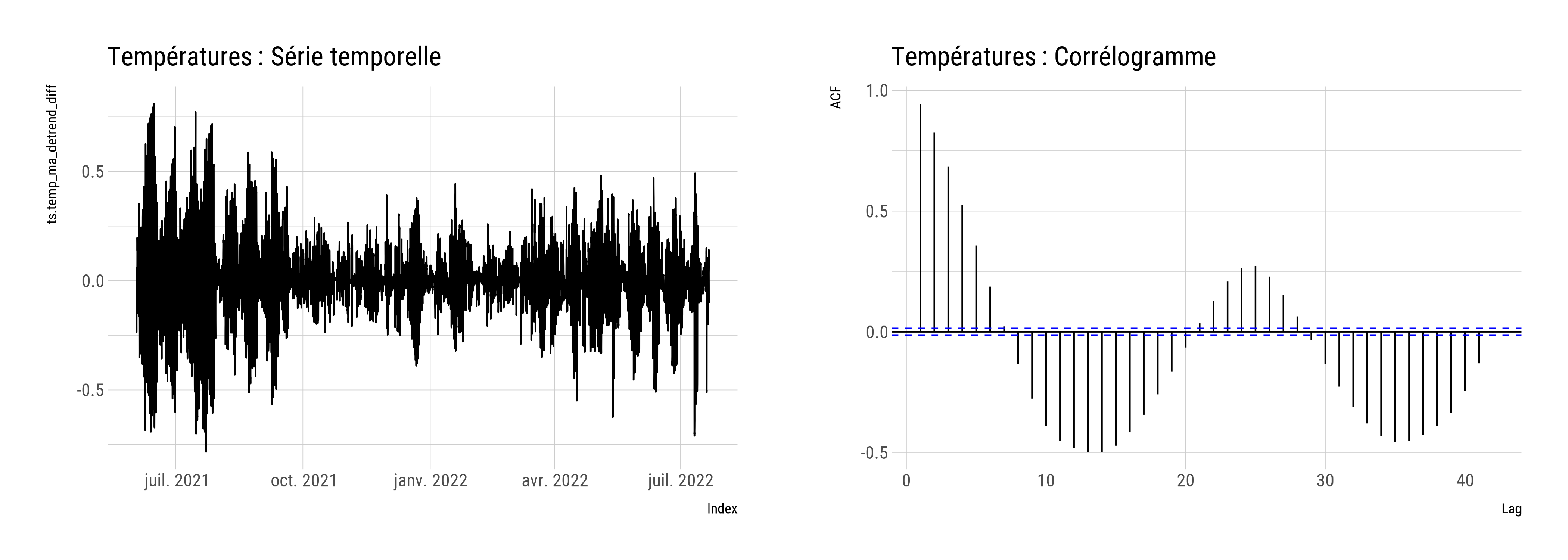
Figure B.9: Série temporelle et autocorrélation du signal de température après différenciation

B.2.4 Conclusion

Les variables explicatives choisies concernant le phénomène de marée (hauteur d’eau à Roscoff, coefficients, vive-eau/morte-eau et dynamique de la marée) ne semblent pas appropriées pour expliquer la variation liée à ce phénomène à l’exutoire de l’étang en raison de la modification du signal de marée à son entré dans l’exutoire de l’étang. Les modèles ont cependant bien fait ressortir l’importance de l’effet du blocage des clapets pour les signaux de hauteur d’eau et de conductivité.

B.2.5 Pistes d’amélioration

Afin de posséder une vision plus précise du fonctionnement des signaux enregistrés à la sonde autonome, il sera nécessaire d’acquérir des données climatiques et hydrologiques à haute fréquence. Une méthode précise d’acquisition des périodes de blocage des clapets semble également indispensable pour affiner les résultats présentés dans ce chapitre. Une nouvelle variable explicative concernant les hauteurs d’eau à l’extérieur de l’étang devra également être calculée afin de remédier aux difficultés dont nous avons discutés.

Il semble également nécessaire d’affiner la méthodologie utilisée dans l’objectif de minimiser la perte d’informations liée aux transformations des signaux.

---

39. L’autocorrélation temporelle est la corrélation qu’un signal entretien avec lui-même.↩︎

40. Une tendance polynomiale dans un signal correspond à une tendance non-linéaire dont la dynamique est régie par un polynôme de degré \(k\). En comparaison, on peut citer les tendances linéaires, exponentielles ou logarithmiques.↩︎